Solving Problems in JavaScript: Recursive vs Iterative
A problem is an obstacle to overcome, once the obstacle circumvented, the problem is solved and we can move on the next one. When we write programs to solve problems, though, we have a larger goal. We don't want to solve just one instance of a particular problem, we want an algorithm that will solve all instances of a problem. A problem is defined by its inputs and the desired output.
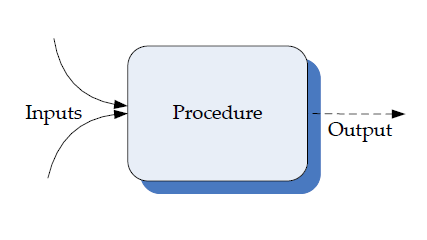
Our goal for solving the problem is to devise a procedure that takes inputs that define a problem instance and produces an output that is the solution to that problem. Most problem solving involves breaking problems into simpler and simpler problems until you find problems simple enough that you already know how to solve. This approach of solving problems by breaking them into simpler parts is known as divide-and-conquer.
Note: An algorithm is a well-defined, computer-implementable instructions, typically to solve a problem or to perform a computation.
Recursive Problem Solving
Recursive problem solving is where a function calls itself again to repeat the code with a goal to reduce the problem to be simple enough. To define recursion, we use an if expression to test the input. If it is true, the consequent expression is the known answer, otherwise, if the test is false, the recursive case applies the procedure again but with a smaller input. For the application to make progress towards reaching the base case, means the input has to change that gets closer to the base case input. The recursion is more used in functional programming.
Recursive Factorial Example
function factorial(number) {
if (number === 1) {
return 1;
}
return number * factorial(number - 1);
}
As we see in the factorial function we have a number parameter which we test with an if statement. If the test is true (the number is 1) we stop the cycle, if the test is false (the number is not 1) we are multiplying the number with the factorial function, which is called by itself.
Note: Factorial is the operation of multiplying any natural number with all the natural numbers that are smaller than it.
Recursive Fibonacci Example
function fibonacci(number) {
if(number <= 1){
return 1;
}else {
return fibonacci(number - 1) + fibonacci(number - 2);
}
}
In our second example is probably one of the most famous algorithms ever Fibonacci sequence. We have a number parameter that we test with an if statement. If it is true, then we return 1 and the cycle ends here. if the test is false we are are going on the next test. Here at the else clause, we have a return statement with two Fibonacci functions which are added with the first one have a parameter number - 1 and the second one number - 2.
Note: Fibonacci numbers, also called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1.
Iterative Problem Solving
Iterative problem solving is based on gradual improvements that loop to repeat some part of the code. To define iteration we use a loop that has a variable that tests the input. If it is true, the loop ends and the answer is known. If the test is false, the loop repeats again and re-evaluate the body expressions of the passed values. For the application to make progress towards reaching the goal, means that the variable that is tested has to change and gets closer to the input. The iteration is more used in imperative programming.
Iterative Factorial Example
function factorial(number){
var result = 1;
for(var i = 1; i <= number; i++){
result = result * i;
}
return result;
}
We can see in the iterative factorial example that we have a number parameter in the factorial function which is not tested with if statement like in the recursive problem solving, but with a control variable value (var i). If our test is false (var i is smaller or equal with the number) we simply multiply the result with the i and update the result variable. When the test is true (var i is smaller or equal with the number), the for-loop ends and we return the result.
Iterative Fibonacci Example
function fibonacci(number){
var a = 1;
var b = 0;
var temp;
while (number >= 0){
temp = a;
a = a + b;
b = temp;
number--;
}
return b;
}
In the second example, we have again Fibonacci sequence but with an iterative way. We have a number parameter and three variables on top. In the while loop again we are doing the testing with a control variable, where we check if it is true (number is greater or equal to 0) then we continue with the loop. Inside the while-loop body we update the temp variable with the value of a, which after we add a and b and update the a variable with the result, and on the next line we simply update the b variable with the value from temp which was taken from the a variable on the first step. On the last line, we are doing decrement to the number which will be tested again. If the test is false(number is not greater or equal to 0) we simply return the b variable.
Note: If you want to learn more about algorithms, I highly recommend you to read this book: Introduction to Algorithms, 3rd Edition (The MIT Press).
Conclusion
The concepts behind the recursion and iteration is to execute a set of instructions (algorithm) repeatedly. The difference between recursion and iteration is that recursion is simply a function call in which the function is being called by itself until a certain condition is met, while iteration is when a loop is repeatedly executed until a certain condition is met. Both recursion and iteration depend on a condition to know when to stop.
Key differences to remember between recursion and iteration:
I hope you can understand how the recursion and iteration work if you find this article helpful please share it.
Tweet